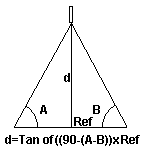Distance Measurement With A Standard Compass

Finding Distance With A Compass

An interesting compass application is to be able to measure the distance across a lake, or large area with a good degree of accuracy. There is an easy way to do this with your compass.

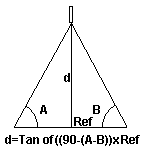
d = (Tan (90 - (A -B))) x Ref

d = Distance (to be calculated)
Tan = Tangent value of the resultant angle
A = Greater value of the two measured bearing angles
B = Lower value of the two measured bearing angles
Ref = Measured reference distance

The method used here is to find a fixed point at the spot you would like to measure the distance from, to where you are. You must sight two reference bearings, one on each end of a measured reference (Ref) distance perpendicular to the spot to be measured. In practice, the more accurate you measure this reference distance, and the greater this distance is up to a 45 degrees total offset, the more exact your results will be.
Please note that the graphic shown here is for demonstration only, and is not calibrated to scale.

• Sight a bearing to the spot that you will measure the distance to, from the exact location where you are standing. This will be bearing or angle (A).
• Walk to a measured perpendicular reference point (Ref) to take another reading to the same spot that will be measured. This will be bearing (B).
• If bearing (B) is greater than bearing (A) then swap the (A) and (B) values. You want to always subtract the smaller number from the greater number.
• Now perform (A) - (B).
• Take this difference and subtract it from 90. Now you have 90-(A-B).
• The next step is to find the Tangent of this final angle or bearing differential. Now you have the Tan of (90-(A-B))
• The last step is to multiply this value by the measured perpendicular reference distance. You now completed the function (Tan(90-(A-B))) x Ref.
• Note that if the first bearing reading is less than 360N (or 0) degrees, and the second bearing reading is past the 360N (or 0) degree value, then you must assume the compass card to exceed the 360N value. For example, if you read 358N degrees for the first value, and 2E degrees for the second value, then the result would be equal to 362 degrees. The differential value would be 4 degrees as required.

For example, if you are looking at a tree across a lake and you want to find its distance from you, sight the first bearing to it. Let us say that it is 210 degrees. Now walk exactly 10 meters perpendicular in relation to the tree (As perpendicular as possible). Next, sight the second bearing to it. Let us say that it is now reading 214 degrees. Now calculate 90 - (214-210). You should get 86. Now find the Tangent of 86. This will give you 14.3 . Multiply this value by the perpendicular reference (Ref) distance (10 meters). This would be (14.3 x 10)=143. The distance (d) to the tree across the lake is 143 meters.

With a very high quality sighting compass, you would be very surprised at the accuracy that can be achieved with this system of measuring distance.

Engineer's Lensatic Compass

There are specialized compasses for specific applications. Some lensatic compass applications are used in industry, the military, and exploration.

The Lensatic Compass Scale was designed to provide a quick way to measure the distance of an object or landmark. It has been worked out to be scaled in 64 units representing the full 360 degrees. However, it offers a slight compromise in accuracy compared to using detailed trigonometry functions. Each division of lensatic angle is equivelent to 5.625 degrees of compass azmuth. The accuracy of distance measurement using the lensatic scale should be within 1% under most applications.

It has been worked out that if a sighted object has a perpendicular width of 1 meter, and measures 1 lensatic division (unit) on the compass scale, it is 10 meters from you.

The formula is: (S / Le) x 10

S = Size of target (perpendicular)
Le = Lensatic divisions, or number of lensatic units

For example, if you have sighted an automobile facing you that you know measures 1.8 meters wide (perpendicular measurement facing you), and the lensatic divisions are 1.6, the distance from you would be: (1.8 / 1.6) x 10 = 11.25 meters from you.

The reading of 1.6 divisions lensatic is equal to 9 degrees of azmuth. Using some basic trigonometry reveals the car to be 11.36 meters distance. The error in this case is about 0.9%. For most applications, and considering possible parallax errors when using a compass, this is considered acceptable accuracy.

Using The Compass Clinometer Scale To Find Height

Here is a simplified way to find the height of a structure or tree. This method applies to compasses that have a clinometer scale. If your compass clinometer scale is in degrees only, you must convert this to the percent of angle (% Grade).

• Measure the total Vertical Angle in percent (% Grade) from the base of the structure to its top. If your compass does not have the % Grade scale, use degrees. You will have to look up the Tangent Value, and convert it to % Grade.

• Measure the Distance from your position to the base of the structure.

• Multiply the Distance by the % Grade.

• Divide this result by 100.

Height = (d) x (%G) / 100

d = Distance
%G = Angular Percentage (% Grade)

To find Percent Grade (%G) from the Tangent Value, multiply the Tangent Value by 100.

%G = Tan x 100

%G = The Percent Grade or Angular Percentage
Tan = The Tangent Value

For example, say the distance to the tree is 100 feet and the %Grade is 30%. The tree height is:

height = 100 feet x 30% Grade / 100 = 30 feet tall ((100 x 30) / 100) = 30
(The measured angle was 17 degrees. Tan 17 = 0.30).

If the Tangent is at or exceeds 100% (45 degrees), then use the direct Tangent value. For example if the angle is 60 degrees, the Tangent value is 1.73. You would use 1.73 directly. In this case the formula is: Height = (d) x Tan.

Tangent / Degree Ratio Table